Nous avons découvert précédemment les grands principes du Machine Learning. Nous allons maintenant présenter comment un modèle simple de régression linéaire permet de formuler des recommandations en vue de faciliter un processus de décision.
Avertissement : cet article contient du code pouvant heurter la sensibilité des plus jeunes.
Sommaire
Présentation du cas
Vous êtes People Analyst de la société Cass&Roll qui fabrique des casseroles dans le Jura. La campagne d’entretien annuelle bat son plein.
Vous avez donc reçu de la plupart des managers :
- Les évaluations sur les soft skills, les hard skills, et la performance globale,
- L’inscription à un programme talent, dont l’objectif est d’assurer la rétention des compétences et potentiels de l’entreprise. Cliquez ici pour découvrir comment formuler des recommandations sur l’inscription au programme talent avec une classification.
- La répartition des augmentations individuelles sur l’année
Cependant, un manager ne vous a transmis que les évaluations. En effet, il n’arrive pas à prendre de décisions (on en connaît tous un comme ça !).
Nous allons tenter ensemble de lui formuler des recommandations à partir des informations qu’il a pu nous fournir.
Exploration des données
Nous commençons par importer les bibliothèques que nous allons utiliser et télécharger les données.
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pylab as plt
import matplotlib.patches as mpatches
data ="https://raw.githubusercontent.com/ArnaudCoulon/MyPeopleAnalytics.fr/main/Analytics/introduction_ML/Database_intro_ML.csv"
df = pd.read_csv(data)Puis nous affichons les types de données et les dimensions de notre base.
print(df.dtypes)
print(df.shape)
Anticiper des augmentations individuelles
Démarche de la régression
A partir de nos données, nous pouvons afficher un graphique représentant le lien entre son taux d’augmentation et sa performance globale.
sns.scatterplot(x="Performance globale",y="Augmentation", data = df)
Il semble qu’à partir d’une performance globale supérieure à deux, il semble exister un lien entre performance globale et taux d’augmentation. Ce lien pourrait être représenté par une droite :
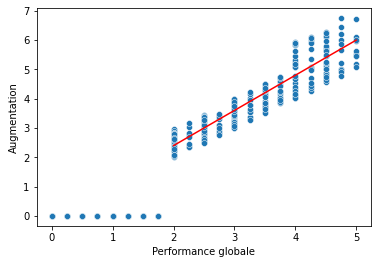
C’est exactement le principe de la régression : identifier une fonction mathématique permettant d’approximer le lien entre plusieurs variables. La courbe rouge représente la fonction que nous souhaitons décrire.
Mise en pratique
Pour mettre en place une régression linéaire, il est possible d’utiliser python :
# Défintion des valeurs à expliquer et valeurs explicatives.
y_reg = df["Augmentation"].values.reshape(-1, 1)
X_reg = df["Performance globale"].values.reshape(-1, 1)
# Import de la bibliothèque Scikit Learn permettant de faire des régressions linéaires.
from sklearn import linear_model
reg = linear_model.LinearRegression()
# Exécution de l'entrainement de la régression linéaire
reg.fit(X_reg,y_reg)Les résultats de la régression linéaire forment une fonction du type :
Y = aX + b
Où :
- Y est la donnée que l’on souhaite expliquer ou prédire, le taux d’augmentation dans notre cas
- X est la donnée explicative, la performance globale dans notre cas
- a est le coefficient de notre fonction mathématique, le rapport de croissance qui existe en Y et X
- b est l’ordonnée à l’origine de notre fonction, la valeur que prend Y lorsque X est nul
Il est possible d’obtenir ces informations avec python :
# Affichage des coefficients de la courbe
print(reg.coef_)
#affichage de l'ordonnée à l'origine
print(reg.intercept_)
Il est possible de représenter la courbe calculée par la régression
#Attribution de la valeur des coefficients et ordonnées à l'origine à des variables
a = reg.coef_
b = reg.intercept_
#Traçage du graphique
sns.scatterplot(x="Performance globale",y="Augmentation", data = df)
x_plot = np.linspace(0,5,100)
y_plot = (x_plot*a+b).reshape(-1, 1)
plt.plot(x_plot, y_plot , color='r')
A ces résultats propres à la fonction s’ajoute le coefficient de détermination (ou R2). Cette mesure permet de juger de la qualité d’une régression linéaire. Cette donnée peut être obtenue de la sorte :
# Affichage du R2, le score de la régression linéaire
print(reg.score(X_reg,y_reg))
Notre modèle permet d’expliquer 89% de la variation des points. C’est un bon score mais il n’est pas parfait. En effet, lorsque l’on revient sur notre graphique, on observe trois groupes :
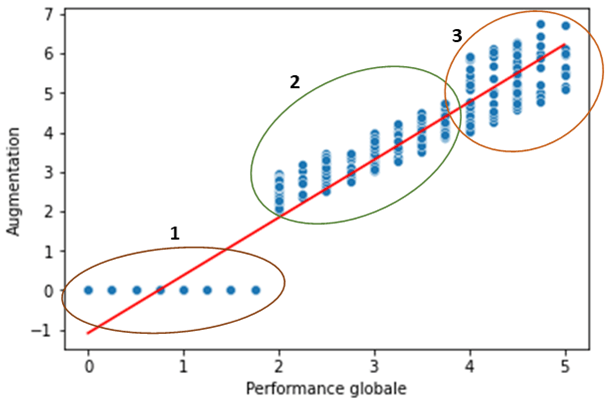
- Le groupe 1 : correspond à des individus pour lesquels aucune augmentation n’est prévue. Néanmoins notre modèle propose une augmentation pour les performances individuelles faibles.
- Le groupe 2 : semble correspondre à la prédiction de notre modèle
- Le groupe 3 : présente des données plus dispersée que le groupe 2, ce qui risque de diminuer la qualité de nos prédictions.
Mise en œuvre des prédictions
Nous allons maintenant utiliser les données de performance que le manager nous a fournies afin de lui formuler des propositions d’augmentations individuelles.
#Téléchargement et lecture des données à prédire
data_to_predict = "https://raw.githubusercontent.com/ArnaudCoulon/MyPeopleAnalytics.fr/main/Analytics/introduction_ML/DataSet_introduction_ML_Echantillon.csv"
df_to_predict = pd.read_csv(data_to_predict)
#Définition des valeurs explicatives et mise en calcul dans notre modèle
X_predict_reg = df_to_predict["Performance globale"].values.reshape(-1, 1)
y_reg_predict = reg.predict(X_predict_reg)
#Représentation graphique de la prédiction
X_reg = df["Performance globale"]
plt.scatter(X_reg, y_reg)
plt.scatter(X_predict_reg, y_reg_predict, color="red")
plt.plot(X_predict_reg, y_reg_predict, color ='green')
plt.show()
On constate que, malgré le bon résultat, les groupes que nous avions identifié influencent bien notre modèle. Cette approximation est particulièrement vraie pour les performances inférieures à deux.
Nous pouvons ensuite afficher les taux d’augmentation prédits afin de les partager avec le manager.
#Affichage des données prédites
print(y_reg_predict.T)
Conclusion
La régression linéaire est un algorithme simple et puissant. Pour l’utiliser, il est important de travailler sur des représentations graphiques afin de bien s’assurer que ce modèle est pertinent. Comme toujours, l’apprentissage machine doit être contrôlé par l’intelligence humaine afin d’assurer sa pertinence dans le contexte.
Nous aurions pu par exemple retirer de nos données les performances inférieures à deux.
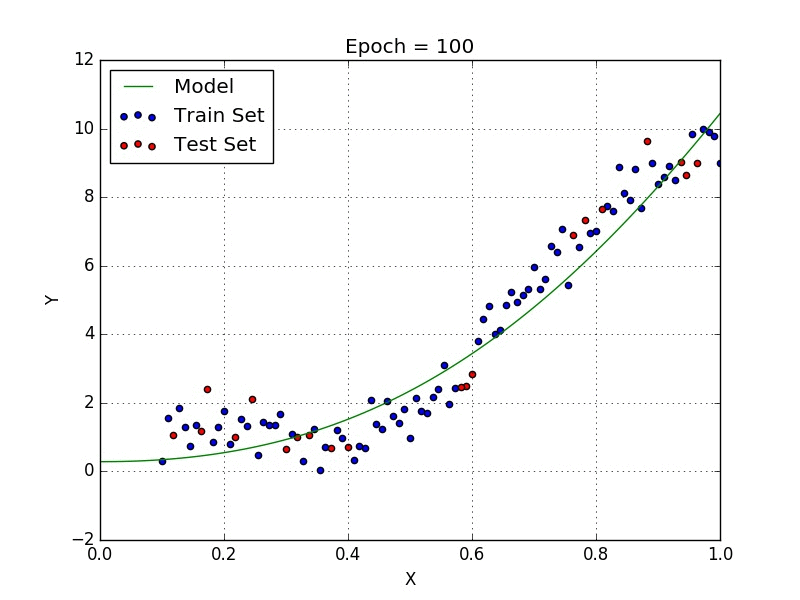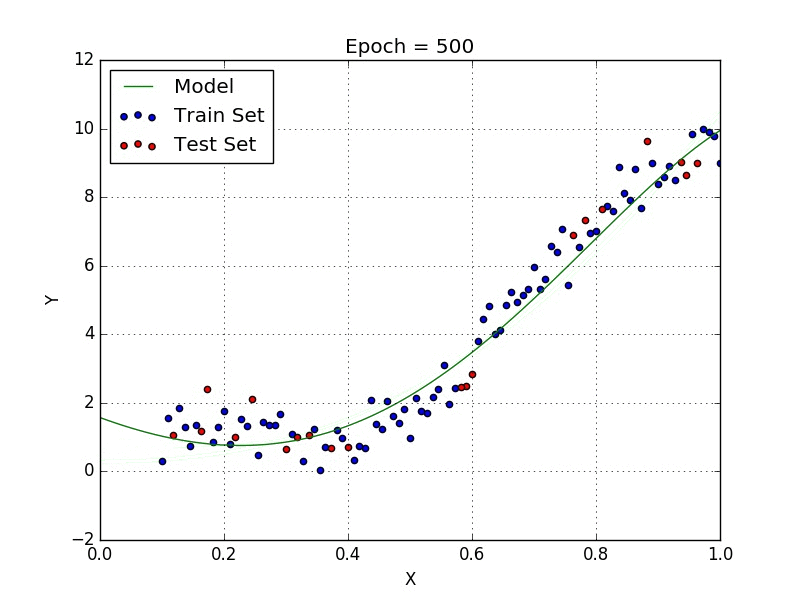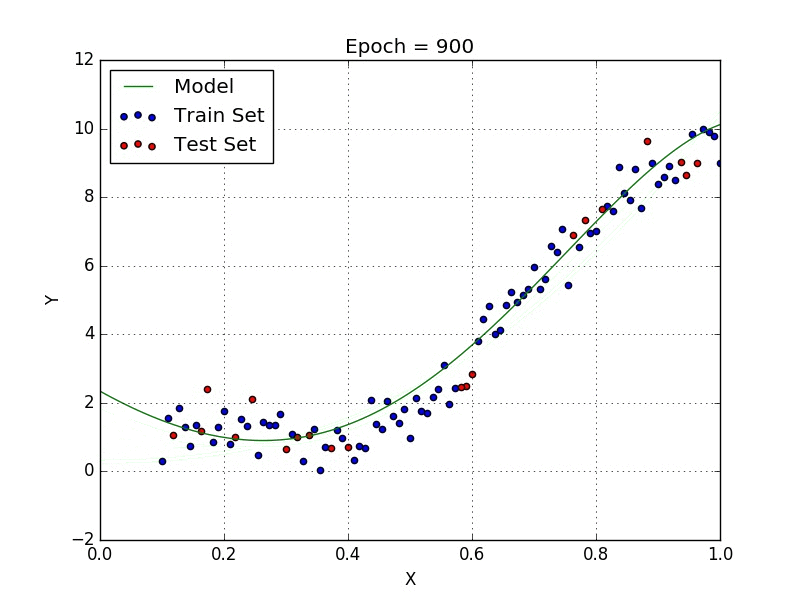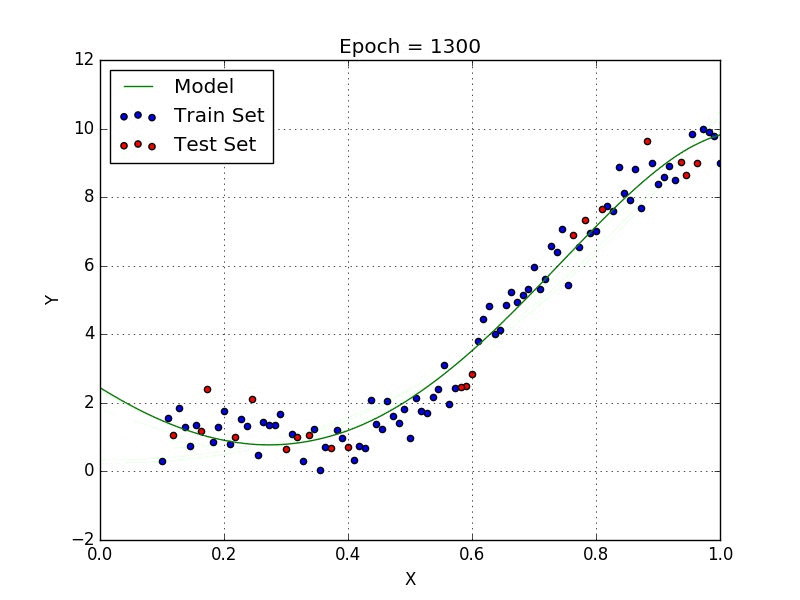
De même, il existe des algorithmes comme la régression polynomiale qui permettent de proposer des fonctions plus complexes comme l’explique la représentation ci-dessous :